

NavMesh(Navigation Mesh)를 만들어보자.

NavMesh란?
NavigationMesh의 줄임말로, 게임내에서 걷고, 뛰고, 뭐 별 짓을 다 할 수 있게 하는 구역을 설정하는 시스템을 말한다.
왜 쓰나? '그냥 플레이어 월드에 띄워 놓고 대충 걸어다니다가 벽이랑 충돌 처리 해서 못가게 하면 되지 않나?'
라고 물어보면 ㅇㅇ 그렇게 해도 된다. 그렇게 해도 게임 만드는데 아무 문제 없다고 생각한다.
근데 이렇게 하면 모든 벽에 Collider를 다 씌워서 매 프레임 플레이어와 충돌 계산을 해야한다. 게임내에 플레이어만 있나? 그렇지 않음.
그래서 NavMesh를 사용하는데 (본인 피셜) 미리 이동가능한 영역을 설정해두어서 불필요한 충돌 처리를 최소화 하고 애초에 게임내에 이동가능한 영역과 아닌 영역을 프로그래머가 관리할 수 있게 하는데 장점들이 있는 듯하다.
NavMesh 안과 바깥 구분
NavMesh를 구현하려면 내적, 외적을 알아야한다. ㅂㄷㅂㄷ...
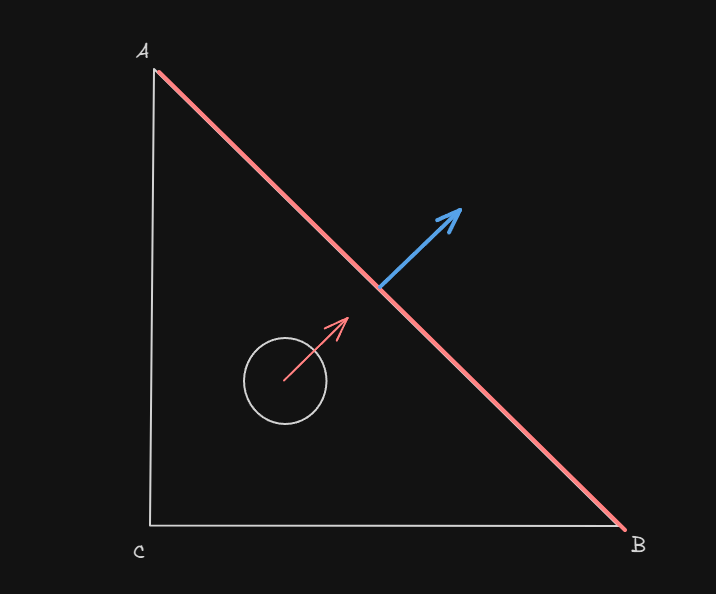
우선 삼각형을 만들었다고 가정하고 이 삼각형안에 플레이어가 있다고 치자. 그리고 빨간 화살 표 방향으로 이동을 하는 중이라고 하자.

이때 플레이어가 삼각형 안에 있으면 그대로 이동시키고, 밖에 있으면 이동을 못하게 막는 것이다.
이게 NavMesh 핵심 개념이다.
삼각형 안에 있는지 밖에 있는지 확인할 때 내적을 쓴다.
두 벡터가 정규화 되었다고 했을 때, A, B둘다 크기가 1이기 때문에 내적의 결과는 Cos그래프의 성질을 띈다.


0~90일때, 양수, 270~360도 이면 양수이다. 반대로 90~270도 사이면 음수인데 이것을 사용하는 것이다.

파란색은 삼각형의 한 면의 수직인 법선 벡터, 초록색은 삼각형 한 정점에서 플레이어를 향하는 방향 벡터이다.
파란색 방향벡터(정규화 됨), 초록색 방향 벡터를 내적해보자. 결과값은 음수이다.
그럼 안에 있는 것이다.
이제 반대로 밖에 있었다고 해보자.
마찬가지로 두 벡터를 내적하면 양수가 나온다.


벡터의 위치는 상관없으니 이렇게 옮겨서 확인해보면 알 수 있다.

1, 2, 3 번 순으로 각 삼각형의 면에 해당하는 법선 벡터와 삼각형 각 정점에서 플레이어를 향하는 방향 벡터를 1, 2, 3순으로 내적해서 모든 결과가 음수라면 삼각형 안에 있는 것이고 결과중 하나라도 양수가 나온다면 삼각형 바깥에 있다고 할 수 있다.
1, 2, 3 내적 연산 순서와 방향 벡터 dot 법선 벡터 이든 법선 벡터 dot 방향 벡터이든 이것도 상관없다. 벡터의 각 성분을 곱해서 더하기 때문에 곱셈 법칙이 적용되기 때문이다.
그럼 문제는 삼각형의 법선 벡텨를 구하는 부분이 남았다.
먼저 점 B에서 A를 빼서 LINE_AB라는 것을 만들어주자. 이 LINE_AB를 정규화 한 뒤 90도 회전 시키면 LINE_AB에 대한 수직인 법선 벡터를 구할 수 있다.
for (_int i = 0; i < LINE_END; ++i)
{
// POINT_END : 3
// 1번 정점 - 0번 정점
// 2번 정점 - 1번 정점
// 3번 정점 - 2번 정점
_vector vLine = XMLoadFloat3(&m_vPoints[(i + 1) % POINT_END]) - XMLoadFloat3(&m_vPoints[i]);
_vector vLineNormal = XMVectorSet(vLine.m128_f32[2] * -1.f, 0.f, vLine.m128_f32[0], 0.f);
_vector vDir = vLocalPos - XMLoadFloat3(&m_vPoints[i]);
// 내적한다.
// - 내적의 결과값이 양수라면 현재 셀 밖으로 나간 것이라 간주한다.
if (0.f <= XMVectorGetX(XMVector3Dot(XMVector3Normalize(vLineNormal), XMVector3Normalize(vDir))))
{
iNeighborCellIndex = m_iNeighborIndices[i];
XMStoreFloat3(&vOutNormal, vLineNormal);
return false;
}
}
// 내적의 결과값이 양수인 부분에 걸리지 않았다면 현재 셀안에 있는 것이므로 true를 리턴한다.
return true;변수명과 주석을 보면 어떻게 삼각형 한 면의 수직인 벡터를 구했는지 알 수 있다.
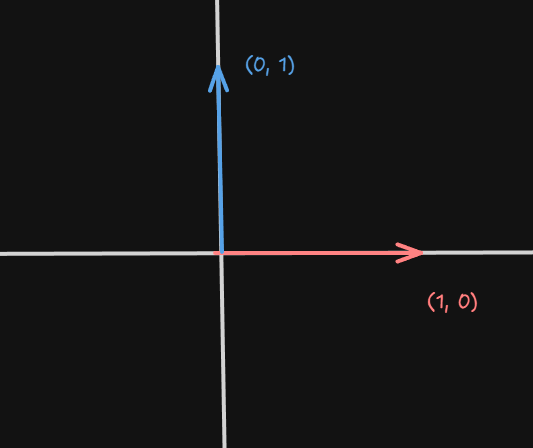
빨간색 벡터를 90도 회전 시키면 1은 0으로, 0은 1로 간다.
즉 x, z 평면상의 수직 벡터를 구하는 공식은 (x', z') = (-z, x)와 같다.
NavMesh 높이 태우기
수직인 벡터는 이렇게 구하면 되는데 여기서 엄청 중요한게 하나 더 있다.
바로 모든 삼각형의 정점을 시계방향으로 통일해서 배치하거나 반시계 방향으로 통일해서 배치해야한다.
왜 그러냐 하면 한 NavMesh위에 플레이어가 서 있으려면 NavMesh가 이루는 삼각형의 한 점의 높이를 알아야한다.

이때 '삼각형을 이루는 면'의 높이를 구할 때 '평면의 방정식'이 사용되고, 평면의 방정식을 사용할 때, '외적'이 사용되기 때문이다.
평면의 방정식을 간략 하게 설명하자면
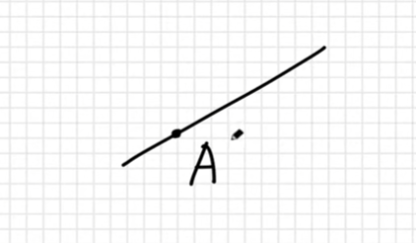
한점 A를 지나는 직선은 수도 없이 많다. 이렇게 수없이 많이 A를 지나는 선들 중에 하나를 정의하기 위해서 '방향 벡터'라는 개념을 사용한다.

즉, 점 A와 평행하면서 방향 벡터 u와 평행한 직선은 오로지 하나이다.

평면에서도 직선에서와 같이, 점 A를 지나는 수많은 선들 중 하나를 골라낼 수 있는 '근거'가 필요하다.
평면에서는 이 근거를 평면에 수직인 벡터로 본다.
이 n이라는 벡터에 수직인 평면은 오로지 하나만 존재한다.
즉, 평면이 어딜 바라보는지를 평면의 수직인 벡터 n으로 나타낸다. 평면의 법선 벡터라한다.
한점과 법선 벡터만 주어진다면 평면 하나를 정의할 수 있다.
점 A를 (x1, y1, z1)이라 하고 법선 벡터 n을 (a, b, c)라 하자. 그리고 플레이어 위치 p를 (x, y, z)라고 하자.
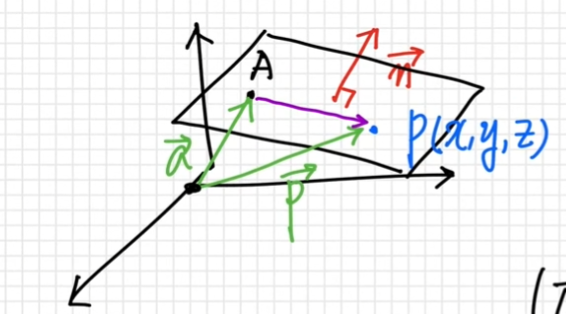
이런 그림이 나오게 된다. AP벡터와 법선 벡터 n을 내적하면 무조건 수직이기 때문에,
AP dot n은 =이다.

AP dot n = 0, (OP - OA) dot n => 이것을 다르게 표현하면 (p - a) dot n = 0이다.

계산하면 결국 위처럼 나오는데 여기서 a, b, c는 법선 벡터 n의 (x, y, z)이다.
그럼 평면에 수직인 법선 벡터를 구해야 하는데 DirectX에서 XMPlaneFromPoints라는 함수를 제공한다.
해당 함수에 점 3개를 넣어주면 이 점에 수직인 법선 벡터를 XMVECTOR로 반환한다.
주의해야할 점이 있다. 인자에 넣는 점의 순서에 따라 법선 벡터가 다르게 구해진다는 것이다.
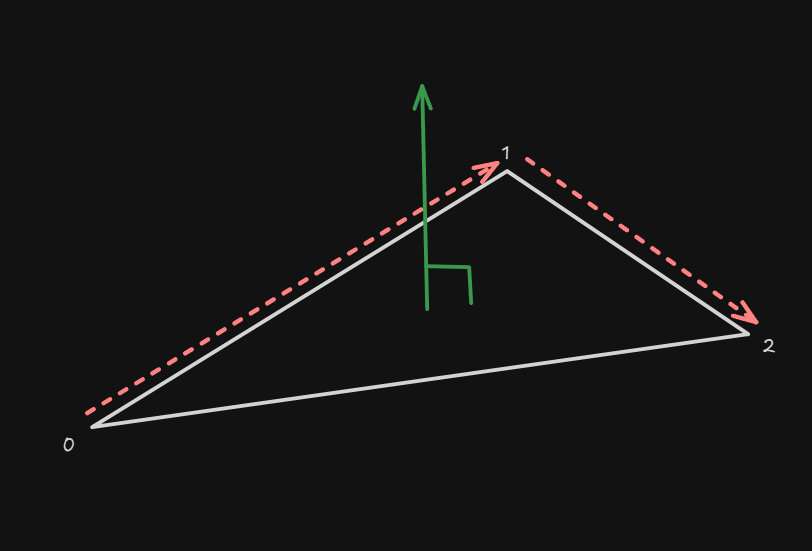
0, 1, 2 순으로 넣으면 '(1 - 0)정점 cross (2 - 1)정점' 으로 초록색 법선 벡터를 반환 하는데
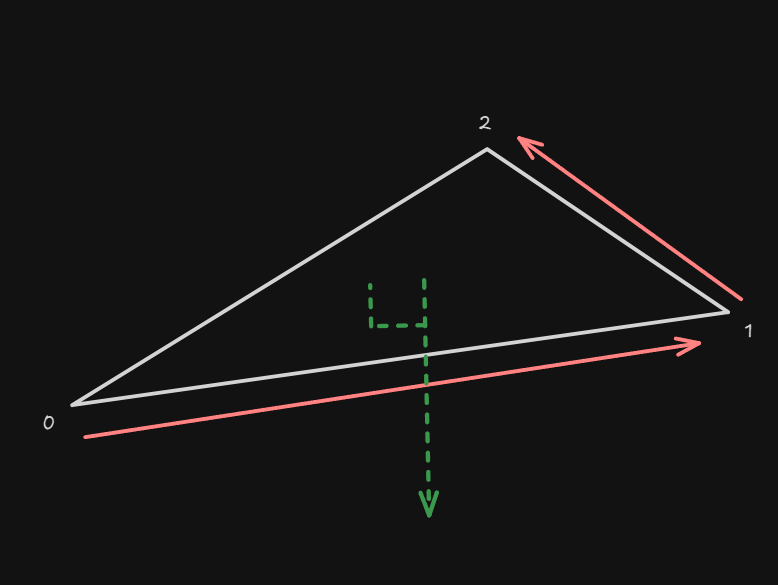
0, 2, 1순으로 집어 넣으면 아래처럼 법선 벡터의 반대 방향이 나온다.
DX는 왼손 좌표계를 따르기 때문에 왼손 법칙에 의해 우리가 기대한 위의 그림처럼 기대한 올바른 법선 벡터가 나온다.
그럼 높이를 구해보자 평면의 방정식 : ax + by + cz + d = 0 이다. 플레이어 위치 p (x, y, z)라하면
XMPlaneFromPoints함수를 사용하여 a, b, c도 알아냈다고 치자. 그럼 y의 값은 y = (-ax - cz - d) / d 를 하면 y값을 알 수 있다.
XMVECTOR vPlane = XMPlaneFromPoints(XMLoadFloat3(&m_vPoints[0]), XMLoadFloat3(&m_vPoints[1]), XMLoadFloat3(&m_vPoints[2]));
return (-XMVectorGetX(vPlane) * XMVectorGetX(vPosition) - XMVectorGetZ(vPlane) * XMVectorGetZ(vPosition) - XMVectorGetW(vPlane)) / XMVectorGetY(vPlane);이렇게 vPlane을 구해서 위의 식대로 그대로 계산을 하여 반환하면 이게 삼각형 평면의 높이가 된다.

'컴퓨터 그래픽스 > DirectX' 카테고리의 다른 글
| 절두체 컬링 (Frustum Culling) (0) | 2024.12.10 |
|---|---|
| [Animation] 애니매이션을 만들어보기 (정리글) (1) | 2024.12.06 |
| [Animation] 스키닝 애니매이션이란? (Skinning Animation) (1) | 2024.11.10 |
| View Spcae Matrix 만들기 (0) | 2024.07.31 |
| [DX] 렌더링 파이프 라인 (5) | 2023.11.30 |

포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!

![[Animation] 애니매이션을 만들어보기 (정리글)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcG82uh%2FbtsK9f6E9CR%2FAAAAAAAAAAAAAAAAAAAAAIFtfsaF0B8pWNr2FNnFn92C-rvUbXZ2fNMClZp_v9Pc%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D3lNjbPqjmAZZqWKe9vXVeON%252FZhE%253D)
![[Animation] 스키닝 애니매이션이란? (Skinning Animation)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcYCMvA%2FbtsKDBOtuN2%2FAAAAAAAAAAAAAAAAAAAAAK7RYh7dkcbluiAvctnEB3FAqf4HaNfsuEHTjyboTBiD%2Fimg.gif%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DvOLL%252BBVS4g2KgKytkvY8Jy7oV6A%253D)
