![[자료구조] 자료구조 Heap 구현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fnz6Sv%2FbtsnLbjB9se%2FAAAAAAAAAAAAAAAAAAAAAGtkDNgkIDPn3RTOV75EktGDD653d1VrgYMuFZr5AaXk%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DJvVrjRvoAi2v6LjOnkqPVEaazmg%253D)

Heap?
힙이라는 자료구조를 알아보기 전에 먼저 "우선순위 큐"가 무엇인지 잠시 살펴보겠습니다.
PQ(우선순위 큐)는 "들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는" 특징을 가지고 있습니다.
즉, PQ는 데이터를 근거로 우선순위를 "판단"할 수 있어야 한다는 말입니다.
이 PQ를 구현을 할때
- 배열을 통해 구현
- 연결형 리스트를 통해 구현
- heap을 통해 구현
이렇게 세가지 정도로 볼 수 있습니다.
배열이나 연결형 리스트를 사용하면 PQ를 매우 간단히 구현할 수 있습니다.
하지만 이들은 PQ를 구현하는데에 있어서 그리 적합하지 않은데요 이유를 설명해드리도록 하겠습니다.
우선 "배열"의 경우 데이터의 우선순위가 높을 수록 배열의 앞부분에 데이터를 위치시킬 수 있습니다.
하지만 std::vector와 비슷? 한 문제점이 존재합니다. 데이터를 삽입/삭제 하는 과정에서 데이터를 한칸씩 뒤로 밀거나 당기는 연산이 동원됩니다.
추가적으로 더 큰 단점은 "삽입 위치를 찾기 위해서 배열에 저장된 모든 데이터와 우선순위를 비교를 진행해야 할 수도 있다."
적절하지 않아 보입니다. 그렴 연결형 리스트의 경우에는 어떨까요??
"연결형 리스트"의 경우 데이터를 삽입/삭제 하는 과정에서 모든 데이터를 한칸씩 밀거나 당기는 연산은 없습니다.(노드 기반이기 때문에)
다만 여전히 배열의 두번째 단점과 동일한 단점이 있습니다. "삽입 위치를 찾기 위해서 배열에 저장된 모든 데이터와 우선순위를 비교를 진행해야 할 수도 있다."라는 문제가 있습니다.
시간 복잡도를 잠시 비교를 해보면
- 배열
데이터 저장의 시간복잡도 : O(n) (우선순위를 정하기 위해 모든 원소들과 비교연산을 진행해야 하기 때문에)
데이터 삭제의 시간복잡도 : O(1)
- 연결형 리스트
데이터 저장의 시간복잡도 : O(n) : 배열과 마찬가지의 이유
데이터 삭제의 시간복잡도 : O(1)
- 힙
데이터 저장의 시간복잡도 : O(Log N)
데이터 삭제의 시간복잡도 : O(Log N)
따라서 저는 "우선순위 큐"를 "heap"이라는 자료구조를 통해서 구현을 할 것입니다!
(우선순위 큐는 Heap으로 구현하고 이 Heap은 배열로 구현할 것입니다)
이제 "힙"에 대해서 설명을 해드리도록 하겠습니다!
"heap"은 "이진트리"이면서 "완전 이진 트리"입니다.
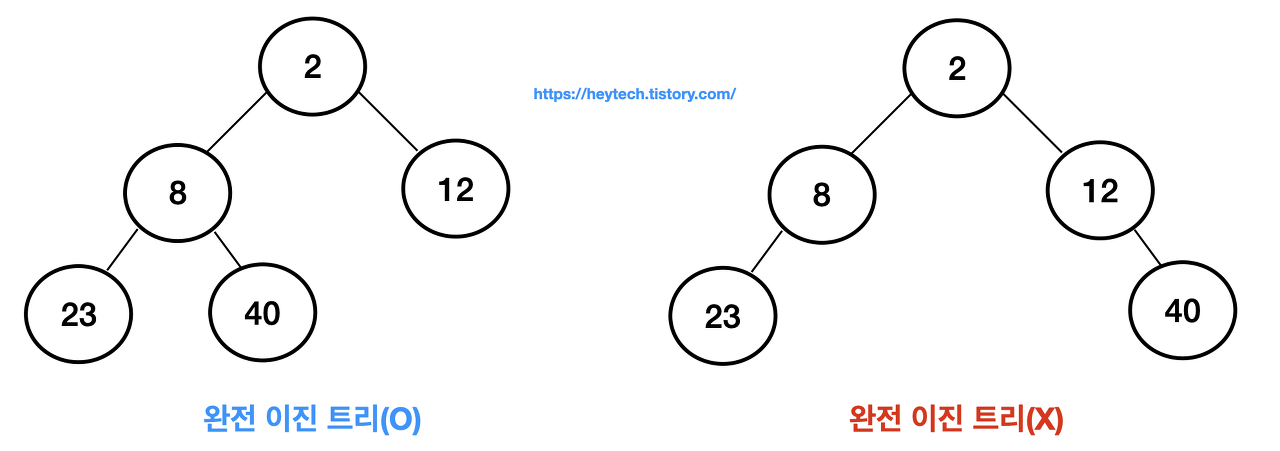
또한 이 heap은 max_heap, min_heap으로 나뉩니다!
여기서 아주 중요한게 힙은 "완전 이진 트리"라는 점입니다! 꼭 기억해 주세요!
힙 구현
우선순위 큐에는 Enqueue, Dequeue 연산이 존재합니다. 따라서 힙을 구현을 할때 우선순위 큐를 기반으로 생각하여 구현을 해보도록 하겠습니다.
먼저 데이터 삽입의 경우
1. "새로 들어온 데이터는 우선순위가 제일 낮다고 가정을 하고 가장 "마지막"위치 에다가 데이터를 저장합니다"
2. "부모 노드와 우선순위를 비교해서 위치가 바뀌어야 한다면 부모와 바꿔줍니다"
3. "계속해서 부모노드와 비교해서 제대로된 위치를 찾을 때까지 1, 2번 반복합니다."
여기서 마지막 위치란? 노드를 추가한 이후에도 완전이진트리가 유지되는 "마지막 레벨의 가장 오른쪽 위치"를 의미합니다.
데이터 삭제의 경우
우선 PQ의 데이터 삭제는 PQ에서 "가장 높은 우선순위의 데이터삭제"를 의미합니다. 그리고 삭제이후에도 힙의 구조를 유지를 해야합니다.
그래서
1. "Root노드 삭제이후 우선순위가 가장 낮은, 즉 가장 마지막 노드의 데이터를 Root노드의 자리로 옮깁니다."
2. 이후 LeftChild, RightChild중에서 우선순위가 높은 자식을 고른다음에 우선순위가 높은 자식과 우선순위 비교를 진행합니다.
3. 만약 여기서 자식이 우선순위가 높다면 부모와 위치를 swap해줍니다. 그게 아니라면 그대로 놔두면됩니다.
(삽입과 마찬가지로 3번에서는 1, 2번을 반복합니다)
힙 구현 고려해야 할점
기능은 이까지 설명을 하도록 하고 그럼 이제 힙을 구현하기전에!
잠시 정리를 하도록 하겠습니다.
우선순위 큐는 "힙"을 통해서 구현해야한다! 라고 제가 이유와 함께 설명드렸습니다.
그렇다면 "힙"은 어떤 자료구조를 통해서 구현해야 할까요?
힙은 "트리"입니다. 트리를 구현하는데 있어서 배열로 구현하는 방법과 연결형 리스트로 구현하는 방법이 있습니다.
둘중에 하나를 골라야 하는데 무엇이 좋을까요?
정답은 "배열"이 구현하기 도 쉽고 "원칙"입니다.
연결형 리스트를 사용해서 힙을 구현할 경우 새로운 노드를 힙의 마지막 위치에 추가하는 것이 어렵습니다.
따라서 배열을 통해서 구현을 하도록 하겠습니다.
특성
구현을 쉽게하기 위해 배열의 0번째 인덱스는 사용하지 않고 1번째 인덱스부터 사용하도록 하겠습니다.
우선 완전 이진 트리이기 때문에 레벨이 하나 증가할 수록 현재 레벨의 노드 수 * 2배씩 원소가 늘어나는 특징이 있습니다.
이러한 특성으로 인해 왼쪽자식 인덱스와 오른쪽 자식인덱스, 부모 인덱스를 쉽게 구할 수 있습니다.
(Root의 인덱스는 1번입니다.)
- 왼쪽 자식 Index : 부모 Index * 2
- 오른쪽 자식 Index : 부모 Index * 2 + 1
- 부모 Index : 자식 노드 Index / 2 (정수 나눗셈이랄 소수는 버립니다. ex) 5 / 2 => 2)
Code
Heap.h
#pragma once
namespace UHeap
{
#define TRUE 1
#define FALSE 0
#define HEAP_LEN 100
typedef char HData;
typedef int (*PriorityComp) (HData d1, HData d2);
typedef struct _heap
{
PriorityComp comp;
int numOfData;
HData heapArr[HEAP_LEN];
} Heap;
void HeapInit(Heap* ph, PriorityComp comp);
bool HIsEmpty(Heap* ph);
void HInsert(Heap* ph, HData data);
HData HDelete(Heap* ph);
int GetHiPriChildIdx(Heap* ph, int idx);
inline int GetParentIdx(int CurrentIdx)
{
return int(CurrentIdx / 2);
}
inline int GetLeftChildIdx(int ParentIdx)
{
return ParentIdx * 2;
};
inline int GetRightChildIdx(int ParentIdx)
{
return ParentIdx * 2 + 1;
};
};
Heap.cpp
#include "UsefulHeap.h"
void UHeap::HeapInit(Heap* ph, PriorityComp comp)
{
ph->numOfData = 0;
ph->comp = comp;
}
bool UHeap::HIsEmpty(Heap* ph)
{
if (ph->numOfData == 0) return true;
else return false;
}
void UHeap::HInsert(Heap* ph, HData data)
{
// numOfData + 1이 heap의 마지막 위치 numOfData는 데이터가 있는 마지막 위치
// 즉 numOfData + 1은 데이터가 들어갈 인덱스(위치)
int idx = ph->numOfData + 1;
while (idx != 1)
{
// 현재 들어온 데이터가 우선순위가 높을 경우
if (ph->comp(data, ph->heapArr[GetParentIdx(idx)]) > 0)
{
// 데이터를 실제로 내림
ph->heapArr[idx] = ph->heapArr[GetParentIdx(idx)];
idx = GetParentIdx(idx);
}
else break;
}
ph->heapArr[idx] = data;
ph->numOfData += 1;
}
UHeap::HData UHeap::HDelete(Heap* ph)
{
UHeap::HData retData = ph->heapArr[1];
HData lastElem = ph->heapArr[ph->numOfData];
int parentIdx = 1;
int childIdx;
while (childIdx = GetHiPriChildIdx(ph, parentIdx))
{
if (ph->comp(lastElem, ph->heapArr[childIdx]) >= 0) break;
ph->heapArr[parentIdx] = ph->heapArr[childIdx];
parentIdx = childIdx;
}
ph->heapArr[parentIdx] = lastElem;
ph->numOfData -= 1;
return retData;
}
int UHeap::GetHiPriChildIdx(Heap* ph, int idx)
{
if (GetLeftChildIdx(idx) > ph->numOfData) return 0;
else if (GetLeftChildIdx(idx) == ph->numOfData) return GetLeftChildIdx(idx);
else
{
if (ph->comp(ph->heapArr[GetLeftChildIdx(idx)], ph->heapArr[GetRightChildIdx(idx)]) < 0)
{
return GetRightChildIdx(idx);
}
else return GetLeftChildIdx(idx);
}
}
main.cpp
#include <iostream>
using namespace std;
#define endl "\n"
#include "UsefulHeap.h"
int DataPriorityComp(char ch1, char ch2)
{
return ch2 - ch1;
}
int main()
{
ios_base::sync_with_stdio(NULL);
cin.tie(NULL);
cout.tie(NULL);
UHeap::Heap heap;
UHeap::HeapInit(&heap, DataPriorityComp);
UHeap::HInsert(&heap, 'A');
UHeap::HInsert(&heap, 'B');
UHeap::HInsert(&heap, 'C');
cout << UHeap::HDelete(&heap) << endl;
UHeap::HInsert(&heap, 'A');
UHeap::HInsert(&heap, 'B');
UHeap::HInsert(&heap, 'C');
while (!UHeap::HIsEmpty(&heap))
{
cout << UHeap::HDelete(&heap) << " ";
}
return 0;
}
중요한 함수들이 몇가지 있습니다.
우선 HInsert, HDelete가 핵심입니다.
HInsert 함수
먼저 HInsert함수부터 분석 해보도록 하겠습니다.
void UHeap::HInsert(Heap* ph, HData data)
{
int idx = ph->numOfData + 1;
while (idx != 1)
{
if (ph->comp(data, ph->heapArr[GetParentIdx(idx)]) > 0)
{
ph->heapArr[idx] = ph->heapArr[GetParentIdx(idx)];
idx = GetParentIdx(idx);
}
else break;
}
ph->heapArr[idx] = data;
ph->numOfData += 1;
}먼저 idx를 가져오는데 포인터로 전달된 ph의 데이터 개수 + 1을 하는 모습을 볼 수 있습니다.
이는 힙이 완전이진트리로 구현되어있고 완전이진트리를 배열로 구현을 하고 0번째 인덱스는 구현을 쉽게하기 위해 사용하지 않고 1번째 인덱스 부터 사용을 하기 때문에 마지막 위치의 인덱스는 numOfData + 1이 되기 때문입니다.
그리고 현재 삽입된 데이터의 우선순위가 부모 노드의 데이터보다 우선순위가 높을 경우
ph->heapArr[idx] = ph->heapArr[GetParentIdx(idx)]를 진행을 합니다. 이는 현재 idx의 부모 노드 인덱스를 가져와 부모노드의 데이터를 현재 마지막 위치(인덱스)로 옮기는 모습입니다.
그리고 나서 idx = GetParentIdx(idx)를 통해 부모 인덱스(위치)를 가져와서 idx로 가져오는 로직인데 실제 데이터를 옮기지는 않고 인덱스만 변경한 것을 확인할 수 있습니다.
위의 로직을 반복(삽입의 3번)을 한뒤 while을 탈출 하게 되면 그제서야 데이터를
ph->heapArr[idx] = data;를 넣어주고 numOfData를 1증가 시켜줍니다.
HDelete 함수
해당함수 또한 완전이진트리의 특성을 적극 활용한 데이터 삭제함수입니다.
먼저 제거될 데이터를 retData에 담아줍니다.
UHeap::HData UHeap::HDelete(Heap* ph)
{
UHeap::HData retData = ph->heapArr[1];
HData lastElem = ph->heapArr[ph->numOfData];
int parentIdx = 1;
int childIdx;
while (childIdx = GetHiPriChildIdx(ph, parentIdx))
{
if (ph->comp(lastElem, ph->heapArr[childIdx]) >= 0) break;
ph->heapArr[parentIdx] = ph->heapArr[childIdx];
parentIdx = childIdx;
}
ph->heapArr[parentIdx] = lastElem;
ph->numOfData -= 1;
return retData;
}그리고 마지막 데이터 lastElem을 가져와 줍니다.
완전이진트리이기 때문에 마지막 데이터는 항상 ph->numOfData값으로 접근을 해서 가져올 수 있습니다.
그리고 while문을 보시면 먼저 GetHiPriorityIdx(ph, parentIdx)보실 수 있는데 해당함수는 parentIdx를 넘겨주었을 때 왼쪽/오른쪽 자식중의 우선순위가 높은 자식의 위치(인덱스)를 반환하는 함수입니다. 이를 childIdx에 대입을 해준 후
함수포인터를 통해 전달된 comp를 통해 누가 우선순위가 높은지 비교를 진행합니다.
comp의 반환값이 0보다 클경우 왼쪽 매개변수가 우선순위가 높다는 뜻이고 0보다 작을 경우 오른쪽 매개변수의 우선순위가 높다는 뜻이며 0일경우 우선순위가 같다는 뜻입니다.
따라서 lastElem과 현재 부모 노드의 자식중의 우선순위가 높은 자식과 비교를 하여 마지막 원소의 데이터가 우선순위가 높다면 break이고 그게 아니라면 로직을 진행합니다.
lastElem의 우선순위가 더 작을 경우에 ph->heapArr[parentIdx] = ph->ph->heapArr[childIdx] 현재 childIdx에 있는 데이터를 부모의 위치로 옮겨줍니다.
그리고 부모의 index는 childIdx로 변경하여 줍니다.(parentIdx = childIdx)
(위의 과정을 반복하여 줍니다. 끝나면 while문을 탈출 합니다)
그리고 while문을 빠져나왔다면 그제서야 힙의 parentIdx위치에 lastElem을 대입하여 줍니다.(적절한 위치를 찾았기 때문에)
그리고 numOfData를 하나 줄여주고 삭제된 데이터값을 반환해줍니다.(return retData)
감사합니다 :)
'자료구조' 카테고리의 다른 글
| [자료구조] Heap (재구현) (0) | 2023.08.15 |
|---|---|
| [자료구조] AVL 트리 (0) | 2023.08.03 |
| [자료구조] 사칙연산 계산기 구현 (0) | 2023.07.04 |
| [STL] Iterator개념과 advance, distance 함수 (1) | 2023.05.21 |
| [자료구조] C++ Vector (손코딩) (2) | 2023.04.16 |

포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[자료구조] Heap (재구현)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FLcbay%2Fbtsq8LceZkK%2FAAAAAAAAAAAAAAAAAAAAANSPME_xpjtma3KpUukSlxhyDBG-VsLrsiDFbDmsRC2S%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DjfLRim%252F10LgJDL9oMRndnKnWk8Y%253D)
![[자료구조] AVL 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fc6lb4Y%2Fbtsp1eSWn7O%2FAAAAAAAAAAAAAAAAAAAAADz9W2gFhM6eqDT3knTDb-O5cUhdEil9bRynE7pUjuVe%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DOqlD%252BF5q3lyIGLsY8FF%252FzRqKJzE%253D)
![[자료구조] 사칙연산 계산기 구현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FpXB60%2FbtsmseCxzh7%2FAAAAAAAAAAAAAAAAAAAAAM0wZxaTKvI0RVabWk99md07C481ZFmMvZjjJbwunu0I%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DhpZmD8YzW9JSjxCgsD5dOfDfg3Q%253D)
![[STL] Iterator개념과 advance, distance 함수](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FmU93S%2FbtsgDJP5KZn%2FAAAAAAAAAAAAAAAAAAAAACDUbdSxnclVUDaNM1kNAupiXtB5xAzIoVSQDvE2H5E9%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D4tdiEeLBXaqIDLiPRpj0zJlKQYY%253D)